Planer surface 물체의 경우에는 3D 공간에서의 2D 이미지로의 임의의 원근투영변환(perspective projective transformation)을 두 이미지 사이의 homography로 모델링할 수 있습니다. 즉, 어떤 planar surface가 서로 다른 카메라 위치에 대해 이미지 A와 이미지 B로 투영되었다면 이미지 A와 이미지 B의 관계를 homography로 표현할 수 있다는 것입니다.
그래서 homography를 planar homography라고도 부르며, homography는 평면물체의 2D 이미지 변환관계를 설명할 수 있는 가장 일반적인 모델입니다. 또한 Homography는 projective transformation과 같은 말입니다.
Homography는 homogeneous 좌표계에서 정의되며 그 일반식은 다음과 같습니다.
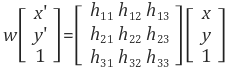--- (18)Homography는 자유도가 8이며 따라서 homography를 결정하기 위해서는 최소 4개의 매칭쌍을 필요로 합니다. Homography의 자유도가 9가 아니라 8인 이유는 (x,y,1), (wx',wy',w)이 homogeneous 좌표이므로 homography의 scale을 결정할 수 없기 때문입니다 (∵ homography 변환 X'=HX에서 X, X'은 homogeneous 좌표이기 때문에 X'=kHX도 성립하게 됩니다. 즉, H가 homography 행렬이라면 임의의 0이 아닌 k에 대해 kH도 또한 동일한 homography 행렬이 됩니다).
주어진 매칭쌍들로부터 homography를 실제 구하는 과정에 대해서는 Elan Dubrofsky, "Homography Estimation", 2009 글을 참조하기 바랍니다. Homography를 구할 수 있는 다양한 방법들이 잘 정리되어 있습니다.
Homography를 직관적으로 이해하기 위한 한 좋은 방법은 2D 평면에서 임의의 사각형을 임의의 사각형으로 매핑시킬 수 있는 변환이 homography다 라고 생각하는 것입니다. 물론 사각형이 뒤집혀질 수도 있습니다.
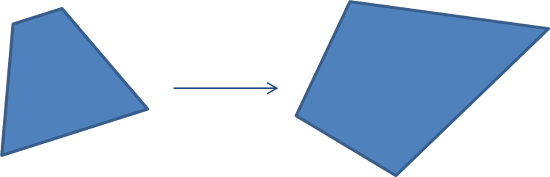
<그림 4>
앞서 설명한 [컴퓨터 비전에서의 Geometry #3] 2D 변환 (Transformations)에 대한 보완 글입니다.
앞서 #3 글에서는 두 이미지 간의 2D 변환 모델에 대해 전반적으로 다뤄 보았습니다. 그런데, 앞 글에서도 언급하였지만 affine 변환과 homography는 아래 그림과 같이 비정상적인 형태로 변환이 구해질 수가 있습니다.
뒤집힘(reflection)은 affine, homography에서 모두 발생할 수 있으며 뒤틀림(twist), 오목(concave)는 homography에서만 발생할 수 있습니다.
이들을 비정상적인 형태라 한 이유는 우리가 3차원 공간에서 아무리 물체를 회전시키고 위치를 변경해도 오른쪽 형태와 같은 영상이 나올 수 없기 때문입니다. 물론 뒤집힘의 경우는 발생은 가능하지만 패턴매칭 관점에서는 역시 비정상적인 상황입니다. 평면물체의 모든 3D 변화는 homography로 표현할 수 있지만 반대로 모든 homography 변환이 실제 영상에서 일어날 수 있는 변환인건 아닙니다.
다음은 위와 같은 비정상적인 변환이 발생할 수 있는 시나리오입니다. 영상에서 도로 표지판을 검출하는 알고리즘을 개발하고자 합니다. 먼저, 표지판에 대한 영상에서 특징점(sift, surf 등)을 추출하여 DB에 저장해 둡니다. 이제 입력 영상에서 특징점을 추출한 후에 DB에 저장된 특징점들과 매칭을 수행합니다. 매칭된 특징점들 사이의 변환관계를 RANSAC(RANSAC의 이해와 영상처리 활용 참조)을 이용하여 affine이나 homography로 근사합니다. 이 때 구해진 변환관계는, 원래 매칭이 잘못되었거나 또는 RANSAC이 실패한 경우 위와 같은 뒤집힘, 뒤틀림, 오목 등이 빈번하게 발생합니다.
한 해결법은 구해진 변환이 위 경우(뒤집힘, 뒤틀림, 오목)에 해당하는지를 검사하여 만일 그렇다면 매칭에 실패한 것으로 판단하는 것입니다.
정상적인 변환인지 여부를 판단하는 방법은 다음과 같습니다.
구해진 (h9=1이 되도록 normalized된) 2D homograpy 변환이 다음과 같다고 했을 때,
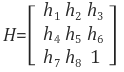--- (1)보통 다음 조건을 하나라도 만족하면 비정상적인 변환으로 판단합니다.
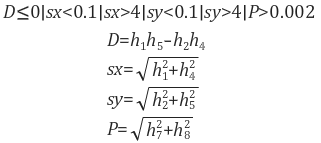___ (2)식 (2)에서 D는 처음 2×2 부분행렬([h1 h2; h4 h5])의 행렬식 값(determinant)이고 sx는 x축 스케일 팩터(scale factor), sy는 y축 스케일 팩터, P는 perspective 정도를 나타냅니다.
Homogeneous 형태로 표현된 3×3 2D 변환행렬에서 처음 2×2 부분행렬은 회전, 스케일, shearing, reflection 파트를, [h3, h6]는 평행이동(translation)을, h7, h8은 원근(perspective) 변화를 나타냅니다.
D<0라 함은 점들 사이의 회전 순서가 지켜지지 않았음을 의미하며 뒤집힘 또는 뒤틀림이 발생했음을 의미합니다. sx는 처음 2×2 부분행렬에 의해 x축 단위벡터 [1 0]T가 얼마나 길이가 변했는지를 나타내며 sy는 y축 단위벡터의 길이(scale) 변화를 나타냅니다. 위 조건식에서 sx, sy < 0.1은 원래 물체의 크기에 비해 너무 스케일이 작아졌는지 여부를, sx, sy > 4는 너무 켜졌는지를 검사하는 것입니다. 식 (2)에 있는 스케일 조건은 참고용일 뿐이며 자신의 문제에 따라서 정상 범위를 적절히 조절하면 됩니다. 마지막으로 P는 perspective 효과(사각형이 사다리꼴로 되는 것)가 난 정도를 나타내는데, 이 값이 0이면 perspective 효과가 전혀 나타나지 않음을 의미합니다. 즉, P>0.002는 perspective가 너무 심하게 일어난 경우를 비정상적인 경우로 간주하겠다는 의미이므로 문제에 따라서는 이 조건을 사용하지 않아도 무방합니다 (또는 threshold를 적절히 조절하여 사용해도 됩니다).
단, 오목(concave)한 경우는 위 D<0 조건으로는 검사가 되지 않습니다. 오목한 경우를 알아내기 위해서는 (0, 0), (1, 0), (0, 1), (1, 0) 네 점을 처음 2×2 부분행렬로 변환시킨 후 변환된 결과가 오목한지 여부를 검사해야 합니다. 오목 여부의 판단은 [수학 이야기] - 다각형 도형의 면적(넓이) 구하기 글을 참고하세요.
Affine 변환의 경우에는 h7 = h8 = 0인 경우로서, P는 항상 0입니다. 따라서, affine 변환이 정상적인지 여부는 D, sx, sy를 구해서 위와 마찬가지로 조건을 검사하면 됩니다.
댓글 없음:
댓글 쓰기